🌸 1. 로그란 무엇인가?
내가 이걸 좀 쉽게 설명할게, 종이를 접는다고 상상해보자, ‘너 이거 몇 번 접었니?’
- 너에게 아주 커다란 종이가 있어요.
- 이 종이를 반으로 접으면, 크기는 절반이 되죠.
- 또 한 번 접으면? 다시 절반.
- 계속 접다 보면, 처음 크기에서 엄청 작아지겠죠.
그런데 이제는 거꾸로 물어볼게요:
“이 종이가 이렇게 작아졌는데, 몇 번 접은 거야?”
이게 바로 로그(Log) 라는 것입니다.
- 곱하기의 결과를 보고
- 몇 번 곱한 건지 거꾸로 묻는 거예요.
글1: 소리란 무엇인가? - 소리의 정의 및 기본 개념
글2: 소리의 물리학 - 파동의 개념과 소리의 본질
글3: 소리의 물리학 - 소리의 특성과 원리, 소리의 3요소
글4: 고유 진동수와 공명: 자연의 울림을 이해하다
글5: 보컬 공명: 공명(Resonance) vs 공진(Sympathetic Vibration)의 음악적 이해
글6: 소리의 반사(Reflection), 잔향(리버브, Reverb)
글7: 소리의 생애를 그리다: Attack부터 Release까지, ADSR 완전 이해하기
글8: 리버브와 딜레이, 에코의 차이: 소리는 왜 울리는가 – 리버브, 딜레이, 에코의 모든 것
글9: 물리적 소리 이론에 의한 심벌의 소리 분석: 라이드 심벌, 차이나 심벌, 크래시 심벌 2, 라이드 벨의 차이 및 용도
글10:소리의 크기, 세기, 음압의 차이? 데시벨 단위: dB, dB SPL, dBFS
글11:소리의 위상(Phase)과 보컬 더블링 방법 (1), 보컬 더블링 패닝, 믹싱
글12:소리의 전달 방향, 탄성파와 전자기파, 횡파와 종파
🌸 2. 로그 값이란 말은 들어봤죠?
곱셈은 어떤 수를 반복해서 더 키우는 일이에요.
예를 들어, 2 × 2 × 2 = 8
그럼, 거꾸로 물어보면:
“2를 몇 번 곱해야 8이 돼?”
👉 답은 3번 (2 × 2 × 2)
그래서 우리는 이렇게 씁니다:
log₂(8) = 3이건 이렇게 읽어요:
“밑이 2인 로그, 8의 로그 값은 3이다.”
“2를 세 번 곱하면 8이 되니까.”
🌸 3. 로그 스케일란?
로그스케일이란: 사다리 대신 ‘계단’이 아니라 ‘점프대’란다.(아래 설명을 잘 들어 보렴)
보통 숫자를 그릴 때는 이렇게 1칸씩 올라가죠:
1 → 2 → 3 → 4 → 5 → ...하지만, 세상에는 이런 것도 있어요:
1 → 10 → 100 → 1000 → ...이건 숫자가 엄청 빨리 커지죠.
이럴 땐 ‘로그 스케일’이 필요해요.
왜냐하면 너무 큰 숫자들은 일반 눈금으론 표현하기 힘드니까요.
로그 스케일은 숫자를 ‘곱하기 기준’으로 나눠보는 눈금자입니다.
- 진짜 눈금자가 1cm, 2cm, 3cm라면
- 로그 눈금자는 1cm, 10cm, 100cm 처럼 곱해지는 간격으로 그려져요.
🌹 예시:
- 🌹 소리의 크기를 나타내는 데시벨(dB)
- 지진의 세기를 나타내는 리히터 규모
- 바이러스 수나 세균 수의 변화 (감염병 그래프)
→ 이런 건 다 로그 스케일로 보아야 진짜 변화가 보입니다.
🌼 정리:
"로그란, 시간의 강을 거슬러 올라가는 노인의 질문이다.
‘도대체 몇 번의 발걸음으로 저 강을 건넜는가?’를 묻는 셈이지."
"로그 값은 무대 위 조명 뒤에 숨어 있는 배우다.
그는 숫자라는 무대에 모습을 드러내지 않지만, 그라는 존재는 뚜렷하다:
- '몇 번의 곱셈이 있어야 저 배우처럼 될까?' "
"로그 스케일은 인간이 상상할 수 없는 거대한 세계를,
작은 A4 용지에 담아내기 위한 신의 눈금자와 같다."
🌼 추가로 알아두면 좋은 몇 가지:
- 로그 함수 (logarithmic function)
예:y = log₂(x)→ x값이 커질수록 y가 천천히 증가하는 함수 그래프 - 로그 성질 (log rules)
로그에도 곱셈, 나눗셈, 제곱과 관련된 규칙이 있어요. 예를 들면:
log(ab) = log(a) + log(b)
log(a^n) = n * log(a)- 밑 변환 공식 (base change formula)
위에서 말한log₂(8) = log(8)/log(2)같은 공식
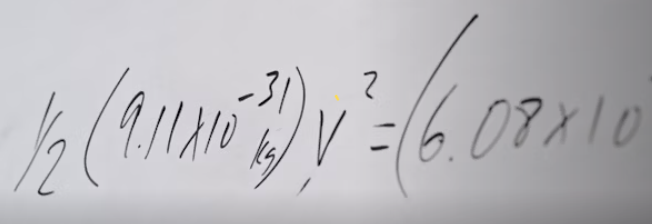
"이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다"